More About the Math:
The Traveling Spike (Part 2)
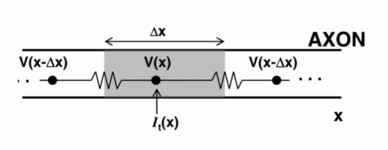
The circuit model for an axon is
To analyze this system, we turn it into another differential equation, with
the solution V (x; t), voltage as a function of time and space,
x measures distance down the axon. Here's how this works, following Mathematical
Biology by James Keener and James Sneyd:
1. The axon, like an electrical cable, can be described as a string of resistors,
each \Delta x\ long. Say the axon resistance per unit length is R.
2. Consider the shaded, \Delta x-long section
of axon. The current flowing in from the left is I_{in} (x)= - \left( V(x) - V(x-\Delta x) \right)/ \left( R \Delta x \right),
the voltage difference divided by the resistance.
3.Similarly, the current flowing out of this section from the right is I_{out} (x)= - \left( V(x+\Delta x) - V(x) \right)/ \left( R \Delta x \right).
4. The difference in inflow vs. outflow currents is due to capacitive and transmembrane currents, say of strength I_t(x) per unit length. That is, I_{in}-I_{out} = I_t(x) \, \Delta x.
Putting these facts together and taking the limit \Delta
x \rightarrow 0 gives:
\begin{eqnarray}
\frac{1}{R} \frac{\partial^2 V(x,t)}{\partial x^2} = I_t(x,t)
\end{eqnarray}
which is a differential equation for V(x,t). In
fact, it's a partial differential equation: it depends both on space
and time.
The currents It are the same as for the Hodgkin-Huxley equations
we studied above:
I_t(x,t)= C \frac{dV(x,t)}{dt} + \bar{g}_{Na}
m(x,t)^3 h (V(x,t)-V_{Na}) - \bar{g}_K n(x,t)^4 (V(x,t)-V_K)
- g_L
(V(x,t)-V_L)
where
\begin{eqnarray}
\frac{dn(x,t)}{dt} &=& \alpha_n(V(x,t)) (1-n(x,t)) - \beta_n(V(x,t)) n(x,t), \\
\frac{dm(x,t)}{dt} &=& \alpha_m(V(x,t)) (1-m(x,t)) - \beta_m(V(x,t)) m(x,t), \\
\frac{dh(x,t)}{dt} &=& \alpha_h(V(x,t)) (1-h(x,t)) -
\beta_h(V(x,t)) h(x,t). \; \;
\end{eqnarray}
Note again that everything, voltages and conductances, now depend on both
space x and time t!
This is quite a complicated system. How can we tell whether it produces
a traveling spike?
CLICK here to SEE HOW HODGKIN AND HUXLEY CRACKED THIS
PROBLEM!