Brain Dynamics:
More about the Math
As we saw above, neural membranes have a potential and during a spike the potential changes
because charged particles flow in and out of the cell through channels. This motivated
Hodgkin and Huxley to model a spiking neuron as an electrical circuit: its voltage changes
over time as currents flow into the cell.
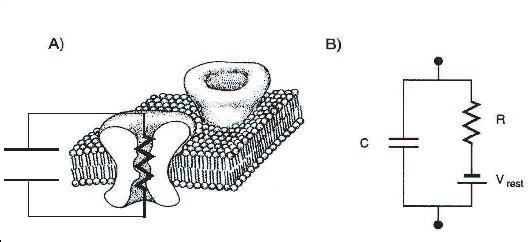
From Bertil Hille, Ionic Channels of Excitable Menbranes, Sinauer Associetes, 1992. (permission pending)
Like all circuits the currents depend on the voltage and also on the permeability (inverse of
resistance) of the cell to charged particles. What Hodgkin and Huxley found in neurons is
that this permeability also changes over time all at a rate determined by the voltage! So we
have an evolving system with feedback:
where F and G are the two ‘Hodgkin-Huxley’ functions. Click
on the equations to see them in their full detail.
An equation like this – based on how variables change over time – is called a differential
equation. The solution is the time course of those variables: for example, the trace of
voltage vs. time in a spike.
One fascinating thing about differential equations is that it’s usually very difficult to guess
even approximately what their solutions will be. In fact, for the Hodgkin-Huxley equations,
nobody has ever been able to write down a formula for the solution on paper - and it probably
will never be done. So what to do? Scientists use are mathematical algorithms that enable
computers (or, for Hodgkin and Huxley, computing machines!) to find the solution. Learn
more about this here: Numerical algorithms
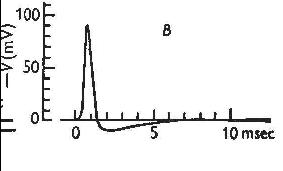
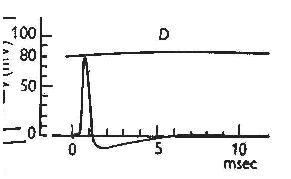
Here’s what Hodgkin and Huxley found when they used these methods to solve their
equations:
| SPIKE IN A REAL NEURON | SOLUTION TO THE HODGKIN-HUXLEY
EQUATIONS |
 |
|
Figures from Hodgkin and Huxley, A quantitative description of membrane current and its application to conduction and excitation in nerve, The Physiological Society, volume 117, 1952; Wiley-Blackwell Publishing.
There it was – the first mathematically generated spike. And this stunning match between
a biology experiment and mathematical theory was the groundwork for Hodgkin and Huxley's
Nobel Prize in 1963.
But, even with this success, much remained unknown about the mathematics of the spike. In fact, much still remains unknown today. We will explore these central questions:
1. What is the geometry of the spike? Surprisingly,
thinking geometrically will solve two of the challenges of the spike we saw
above: Since wildly different cells can spike, is there a robust mechanism
for the spike that's common to these spiking cells? Since neurons behave in
strange ways, for example spiking in response to both positive and negative
inputs, how does a neuron decide when to spike?
2. Once it happens somewhere, how
does a spike travel down a nerve? To
answer this, we need to study states that change in both time and space by
utilizing more complicated mathematical structures called a partial differential
equation.